|
In the realm of understanding, where concepts intertwine like threads in a grand web, the idea of recursion stands as a pillar, echoing the patterns found in nature, mathematics, and the very fabric of reality. This exploration delves into the profound interconnectedness of recursion, the eternal now, unraveling time, fractal understanding, and the cause and effect, woven together in a feedback loop that mirrors the infinite complexity of the Fibonacci sequence. Figure 1. Recursion and the Eternal Now: This figure presents a journey through recursion, the eternal now, unraveling time, and fractal understanding, all linked by cause and effect within an ongoing feedback loop. Inspired by Fibonacci recursion, it shows how each concept fluidly transitions into the next, reflecting universal patterns. This visual exploration invites us on a discovery where time and consciousness blend, unveiling the interconnected weave of reality. The Foundation: Recursion and Fibonacci Recursion, at its core, is a method where the solution to a problem depends on solutions to smaller instances of the same problem. It's a principle beautifully exemplified by the Fibonacci sequence, where each number is the sum of the two preceding ones. This sequence is not just a mathematical curiosity but a pattern that recurs throughout nature, from the spirals of shells to the branching of trees. In our conceptual framework, recursion represents the starting point, the seed from which our understanding of the eternal now begins. It's the process of looking inward, of finding within each moment the seeds of past and future, each now a reflection of the infinite recursion that defines our existence. The Eternal Now: Pure AwarenessAt the heart of our exploration lies the eternal now, a state of pure awareness unbound by the linear constraints of time. It's a concept that transcends the ticking of clocks and the pages of calendars, representing a moment of clarity and presence that is both fleeting and everlasting. This eternal now is not a static point but a gateway to deeper understanding, a lens through which we view the dance of interconnection that binds all things. It's in this eternal moment that we find the essence of recursion, the echo of the Fibonacci sequence in the rhythm of our thoughts and the patterns of our consciousness. Unraveling Time: The Dance of Interconnection From the eternal now, we move to the unraveling of time, a process that reveals the interconnected nature of our experiences and perceptions. Time, in this context, is not a line but a web, a complex weave of causes and effects that defy simple linear explanation. This unraveling is a journey through the fractal complexity of reality, where each moment contains within it the seeds of countless others. It's a recognition that every event, every thought, and every action is part of a greater whole, a symphony of interconnection that resonates with the patterns of recursion and the Fibonacci sequence. Fractal Understanding: Beyond Cause and Effect As we delve deeper into the web of time, we arrive at fractal understanding, a perspective that transcends the traditional linear chain of cause and effect. In this realm, the simplicity of one-to-one relationships gives way to a more fluid, dynamic understanding of how things relate. Fractal understanding is about recognizing the self-similar patterns that recur at different scales, from the microcosm to the macrocosm. It's about seeing the Fibonacci sequence not just in a series of numbers but in the very structure of our thoughts and the universe itself. The Feedback Loop: A Return to Recursion Completing our conceptual journey is the feedback loop, a path that leads from the complexities of fractal understanding back to the simplicity of recursion. This loop is a reminder that in every end is a beginning, in every complexity, a simplicity waiting to be discovered. The feedback loop is the breath of the cosmos, the rhythm of existence that dances to the tune of the Fibonacci sequence. It's a cycle of renewal and understanding that brings us back to the eternal now, enriched by our journey through the unraveling of time and the depths of fractal understanding. Conclusion: The Web of UnderstandingIn this exploration of recursion, the eternal now, and the fractal nature of reality, we find a reflection of the infinite complexity and beauty of the universe. Like the Fibonacci sequence, our understanding unfolds in ever-expanding spirals, each turn revealing new vistas of awareness and connection.
The journey through these concepts is not just an intellectual exercise but a meditation on the nature of existence itself. It's a reminder that in the patterns of the universe, from the smallest shell to the vastness of the cosmos, lies a message of interconnection and eternal renewal, a symphony of patterns waiting to be discovered and understood.
0 Comments
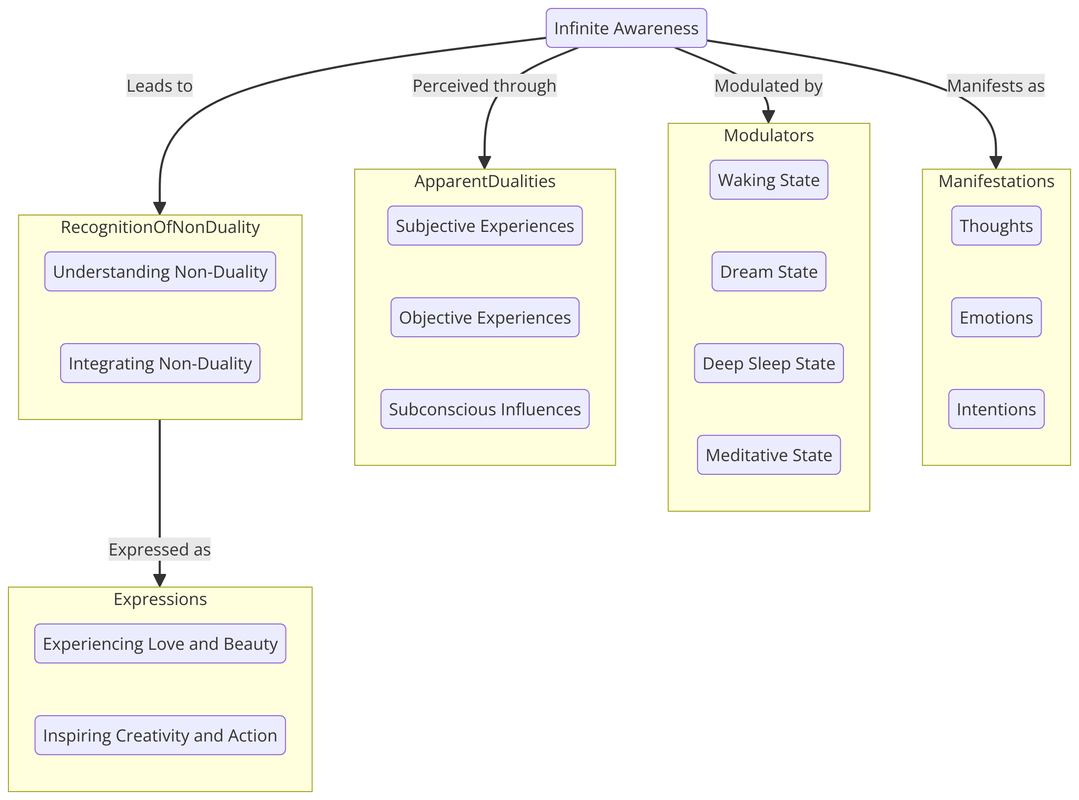
In the vast landscape of human experience, consciousness remains one of the most profound and debated subjects. This blog post delves into a compelling framework that simplifies the complex subject of consciousness into an accessible taxonomy, inviting readers on a transformative journey of self-discovery. Figure 1: The Consciousness Taxonomy This diagram illustrates the simplified taxonomy of consciousness, highlighting the foundational aspect of Infinite Awareness and its various manifestations, modulations, and the recognition of non-duality. The Foundation: Infinite Awareness At the core of this exploration lies the concept of Infinite Awareness, the bedrock of all experience. Unlike the transient states of mind and emotion, Infinite Awareness is constant, unchanging, and ever-present. It is not something we possess but rather what we fundamentally are. This pure consciousness is the backdrop against which the dance of life unfolds, a silent witness to the myriad experiences that constitute our existence. Manifestations of Awareness Awareness, in its infinite potential, expresses itself through various forms:
Modulations of Awareness The taxonomy further explores how awareness modulates itself in different states:
Apparent Dualities within Awareness The journey through consciousness reveals apparent dualities:
Recognition of Non-Duality The pinnacle of this taxonomy is the recognition of non-duality:
Expressions of Non-Dual Understanding When the non-dual nature of reality is recognized, it finds expression in:
Conclusion: A Return to Source This taxonomy of consciousness is not merely an intellectual framework but a roadmap for spiritual exploration. It guides us from the diversity of experiences back to the singularity of our true nature. In recognizing and abiding as Infinite Awareness, we find peace, love, and freedom at the core of our being, where the journey and the destination merge into one.
The Spiritual Journey through the Lens of the Fibonacci Sequence: Insights from Famous Lives12/30/2023 INTRODUCTIONHave you ever wondered if life follows a hidden numerical pattern? Today, we're exploring how the lives of renowned individuals align with the Fibonacci sequence, particularly at the ages of 18, 30, and 49. The Fibonacci sequence, a series of numbers where each number is the sum of the two preceding ones, might just be a key to understanding significant spiritual milestones. What is the Fibonacci Life Chart Method?The Fibonacci Life Chart Method, a concept developed by Sacco (2013), presents an innovative approach that intertwines the progression of the Fibonacci sequence with human developmental patterns. This method offers a fresh perspective on understanding the rhythms of life stages, aging, and spiritual experiences. By aligning the mathematical progression of the Fibonacci sequence with human development, this approach suggests that key aspects of human growth, aging, and spiritual experience may parallel this inherent sequence, characterized by order and predictability. Spiritual Awakenings at Key Fibonacci AgesAround Age 18
Around Age 30:
Around Age 49:
ConclusionThe alignment of these significant spiritual events with the Fibonacci ages is intriguing. It suggests a possible hidden pattern in our spiritual development, a rhythm to our life's journey that resonates with this mystical sequence Your ThoughtsDo you see patterns in your own life that align with the Fibonacci sequence? Share your experiences and insights in the comments below. Let's discover together whether our spiritual journeys are indeed intertwined with this fascinating numerical sequence.
Unveiling the Story Behind The Fibonacci LifeChart Method: A Decade of Discovery and Open Innovation Today, I'm excited to share with you a personal journey that has not only shaped my career but has also led to the creation of a unique concept: the Fibonacci LifeChart Method. This journey intertwines my passion for psychology, an intriguing mathematical sequence, and my commitment to open scientific collaboration. The Spark of an IdeaMy adventure began during my PhD research in psychology. I stumbled upon a fascinating research paper by Norman S. Rose, who discussed using the Fibonacci sequence based on John Waskom's work. Waskom found a natural progression of human development revealing itself. This insight was a revelation. What if we applied the Fibonacci sequence using days instead of years? This single thought ignited a decade-long pursuit of understanding human development, psychology, and even mystical experiences through the lens of the Fibonacci sequence. The Fibonacci Sequence in Human DevelopmentFor those unfamiliar, the Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, starting with 0 and 1. This sequence is not just a mathematical curiosity; it appears in various aspects of nature and now, as my research suggests, potentially in human development. By recalibrating the sequence to days, we could explore human growth and development in a more nuanced and potentially insightful way. This idea was not just a theoretical exercise but a tool – a calculator that could offer a new perspective on how we understand our journey through life. Why I Chose Not to PatentWhen I realized the potential of this calculator, a crucial decision lay before me: to patent or not to patent. After much contemplation, I decided against filing for a patent. Why, you might ask? My goal has always been to contribute to the collective understanding of human psychology and development. I believe knowledge should be shared, not restricted. Patenting, while useful for protecting and commercializing inventions, comes with exclusivity and time limits – typically 20 years. I wanted this calculator to be a tool for everyone – academics, researchers, students, and anyone curious about the application of the Fibonacci sequence in human life. An Open InvitationThis journey has been incredibly rewarding, and the story of the Fibonacci LifeChart Method is still being written. I am committed to continuing this research endeavor and am always eager to collaborate with like-minded individuals. If you are interested in this field or want to be a part of popularizing this calculator, I warmly invite you to contact me. Let's explore the fascinating interplay of numbers and human life together. Looking AheadAs I reflect on the past decade, I am filled with gratitude and excitement for the future. This journey has not only been about developing a calculator but about embracing a philosophy of openness and collaboration in scientific research.
Thank you for being part of this journey, and I look forward to many more years of exploration and discovery. Introduction: Echoes from the PastHave you ever found yourself in a situation that seemed too coincidental to be mere chance? Perhaps you thought of someone you hadn't spoken to in years, and they called you the next day. These events, often brushed off as coincidences, have a name in the realm of psychology: "synchronicities." Coined by Swiss psychologist Carl Jung, the term refers to meaningful coincidences that seem too uncanny to be mere chance. But what if this concept is not as modern as we think? What if ancient civilizations had their own interpretations of these "meaningful coincidences," long before Carl Jung introduced the term? This blog post aims to explore this fascinating idea. We will delve into the ancient world's understanding of what we now call synchronicity. We'll look at how different cultures interpreted celestial events and meaningful coincidences and how these interpretations influenced their decisions and shaped their civilizations. Prepare yourself for an intriguing journey through time. We will traverse through ancient ruins, explore hieroglyphs, and decode cave paintings to uncover the hidden meanings of synchronicity in ancient civilizations. Synchronicity: A Modern Term for an Age-Old ConceptIn today's world, the term "synchronicity" is often associated with New Age philosophies or modern psychology. It's a concept that has found its way into popular culture, self-help books, and even scientific discussions. Carl Jung, who coined the term, described synchronicity as meaningful coincidences that seem too uncanny to be mere chance. He emphasized that these coincidences have no causal relationship; they are connected only by meaning. But let's take a step back and imagine a world without the term "synchronicity." Picture yourself as an ancient Greek philosopher or a Chinese sage. You would undoubtedly observe the same phenomena that we describe as synchronicities today. However, you might interpret them differently. In ancient Greece, these meaningful coincidences were often seen as omens or messages from the gods. The Chinese had their own interpretation, often consulting the I Ching, an ancient divination text, to decipher the meaning behind such events. The concept of meaningful coincidences is not confined to any particular era or culture. It's a universal human experience that transcends time and geographical boundaries. The ancient Egyptians, for instance, saw significant events as the will of the gods manifesting in the physical world. In Hindu philosophy, the concept of "karma" captures a similar essence, where actions and events are believed to be interconnected in a complex web of cause and effect. So, while the term "synchronicity" may be modern, the essence of the concept is ancient. It's a thread that weaves through the tapestry of human history, linking us to our ancestors in a shared understanding of the mysterious events that shape our lives. The Universal Language: Planetary TransitsWhen we talk about language, we often think of words, sentences, and grammar rules. But what if the universe has its own language, a universal code that transcends human speech? For ancient civilizations, this universal language was found in the movements of celestial bodies, particularly planetary transits. The term "planetary transits" refers to the phenomenon where a planet passes across the face of a star, usually the Sun, as seen from Earth. These transits were not just astronomical events to our ancestors; they were powerful synchronistic occurrences that could guide decisions, rituals, and even the destinies of entire civilizations. For example, the Mayans were deeply fascinated by Venus. Its cycles were meticulously recorded and used to time wars and other significant events. This wasn't just a cultural quirk; it was a deeply ingrained belief that the movements of Venus had a direct impact on earthly events. In ancient India, the science of Jyotish, or Vedic astrology, has been used for millennia to choose auspicious dates for weddings, constructions, and even political events, all based on planetary positions. The term "auspicious" refers to moments considered favorable or conducive to success. In Vedic astrology, planetary transits are considered critical for determining these auspicious moments. Even in the Christian narrative, celestial events have played a significant role. The "Star of Bethlehem," which guided the Three Wise Men, is believed by some historians to have been a rare triple conjunction of Jupiter, Saturn, and Venus. This celestial event wasn't just a beautiful sight; it was considered a divine message, guiding the Wise Men to the birthplace of Jesus. So, whether it's the Mayans looking to Venus for war guidance or ancient Indians consulting astrologers for wedding dates, the movements of celestial bodies have been a universal language for humanity. They serve as cosmic traffic lights, telling us when to go, slow down, or stop. And while we may not base our decisions on planetary transits today, understanding this ancient practice can offer us a unique perspective on how interconnected we are with the universe. The Grand Tapestry: Weaving Together the Past and PresentWhen we look at the world around us, it's easy to see it as a series of isolated events, disconnected moments that have little to do with one another. But what if everything is interconnected in a grand tapestry that weaves together the past, present, and future? The term "tapestry" is often used metaphorically to describe a complex or intricate situation. In this context, it refers to the interconnectedness of all things, from celestial events to human experiences. This idea isn't new; it's deeply rooted in ancient philosophies, religious traditions, and even modern scientific theories. Carl Jung, the Swiss psychiatrist who coined the term "synchronicity," was heavily influenced by Eastern philosophies, alchemical traditions, and astrology. Jung collaborated with physicist Wolfgang Pauli to explore the connections between synchronicity and quantum physics. They pondered whether meaningful coincidences might be rooted in the very fabric of reality. The term "quantum physics" refers to the branch of physics dealing with the behavior of matter and light on the atomic and subatomic levels. It's a field that has opened up new ways of understanding the universe, including the possibility that events are interconnected in ways we can't easily see. Even the famous double-slit experiment in quantum mechanics suggests that particles can exist in multiple states until observed. This experiment has led scientists to ponder whether the act of observation itself influences the outcome, a concept that echoes ancient beliefs about the influence of celestial events on earthly occurrences. So, whether you're an ancient Mayan priest interpreting the cycles of Venus or a modern physicist studying quantum entanglement, the underlying message is the same: we're all part of a grand tapestry of existence. And this tapestry isn't just a backdrop; it's an active participant in the unfolding of our lives, offering clues, messages, and guidance if we're willing to pay attention. Conclusion: The Cosmic Dance of DestinyAs we reach the end of this journey, it's time to step back and ponder the bigger picture. We've explored ancient civilizations, modern theories, and the enigmatic concept of synchronicity. But what does it all mean?
The term "destiny" often refers to a predetermined course of events, a path that one is meant to follow. But in the context of the cosmic dance, destiny isn't just about individual paths; it's about the interconnectedness of all things. Whether it's a Mayan priest interpreting the cycles of Venus or a modern physicist pondering the implications of quantum entanglement, we're all participants in a cosmic dance. This dance isn't random or chaotic; it's a choreographed sequence that has been unfolding since the dawn of time. In this intricate dance of planets, stars, and even subatomic particles, we find a timeless message: everything is interconnected, and the universe has always been speaking to us. The term "interconnectedness" refers to the state of being connected with each other, and in this context, it means that nothing exists in isolation; everything is part of a larger whole. So, as we navigate the complexities of life, let's remember that we're not alone. We're part of a grand, cosmic dance, a dance that invites us to listen, learn, and perhaps even lead. And as we step in tune with this cosmic rhythm, we might just find that the universe has been whispering to us all along, offering guidance, wisdom, and a sense of wonder that transcends time and space. Have you ever thought of someone, only to receive a call from them moments later? Or perhaps you've found yourself humming a tune, only to hear it playing on the radio shortly after? These uncanny moments often leave us puzzled, questioning whether they are mere coincidences or something more meaningful. Welcome to the enigmatic world of synchronicity, a concept that challenges our understanding of coincidence and causality. Historical ContextThe Roaring Twenties were a time of great change and innovation. Jazz music filled the air, flapper dancers graced the stages, and groundbreaking ideas were taking shape in the realms of science, art, and philosophy. Amidst this backdrop of transformation, Swiss psychiatrist Carl Jung introduced a revolutionary concept that would forever change the way we think about coincidences: synchronicity. Jung was no ordinary psychiatrist. He was a pioneer who challenged the norms of his time. While his contemporary Sigmund Freud was delving into the unconscious mind, Jung explored the depths of the collective unconscious, introducing groundbreaking concepts like archetypes and the shadow self. But what led him to the idea of synchronicity? And why does it matter? Defining SynchronicityThe term "synchronicity" was coined by Carl Jung to describe the meaningful coincidences that occur in our lives. Unlike cause-and-effect relationships, where one event directly leads to another, synchronicities are events that are related by meaning rather than causality. Imagine two completely unrelated events happening simultaneously, like a cat stretching and yawning just as a city's power goes out. On the surface, these events seem unrelated, but what if they hold a deeper, more mysterious connection? Jung's concept of synchronicity challenges our conventional understanding of the world. It suggests that the universe is not just a mechanical system operating on the principles of cause and effect, but a complex web of meaningful connections. This idea opens up a realm of possibilities, inviting us to explore the mysterious ways in which events in our lives might be interconnected. Contrast with CausalityMost of us are familiar with the concept of cause and effect. We understand the world as a series of dominoes, where one event sets off a chain reaction leading to another. This linear understanding of the world is deeply ingrained in our minds, but synchronicity challenges this conventional wisdom. Imagine a line of dominoes set up neatly on a table. You push the first domino, and it topples the next one, setting off a chain reaction. This is cause and effect in action. Now, imagine another scenario where two dominoes are standing close to each other but not touching. You push one, and the other falls at the same time, even though they never made contact. This is synchronicity—a meaningful connection without direct causality. Jung's Personal ExperiencesCarl Jung's interest in synchronicity was not purely academic; it was deeply personal. One of the most famous incidents that led him to explore this concept was the scarab beetle story. During a therapy session, a patient described a dream she had about a golden scarab, a symbol of rebirth in Egyptian mythology. As she recounted her dream, a scarabaeid beetle tapped on the window, an event too uncanny to be dismissed as mere coincidence. Jung's personal experiences with synchronicity fueled his exploration into this mysterious realm. He believed that these meaningful coincidences were not just random events but messages from the universe, hinting at a deeper connection between all things. Human Nature & Pattern RecognitionHumans are inherently pattern-seeking creatures. From constellations in the night sky to faces in inanimate objects, we are hardwired to find patterns in the world around us. This ability has been crucial for our survival, helping us predict and make sense of our environment. But what happens when this pattern-seeking goes into overdrive? Enter 'apophenia,' the tendency to perceive connections and meaning between unrelated things. This psychological phenomenon raises an intriguing question: Are synchronicities just our brains finding patterns, or is there something deeper at play? Could it be that the universe is whispering secrets to us through these meaningful coincidences? Exploring Examples & Cultural SignificanceSynchronicities have fascinated humans across cultures and historical periods. In ancient China, the simultaneous blooming of cherry blossoms in two distant provinces was seen as a sign of cosmic harmony. Native American tribes interpreted the sudden appearance of animals like ravens as spiritual guidance. These examples highlight a universal human tendency to seek meaning in coincidences. Different cultures interpret synchronicities in various ways, but the underlying theme remains the same: a belief in the interconnectedness of all things. Whether seen as messages from the universe, spiritual guidance, or ancestral communications, synchronicities invite us to ponder the deeper implications of these uncanny events. Scientific Skepticism & DebateThe concept of synchronicity has its fair share of skeptics, especially in the scientific community. Critics argue that synchronicities are not scientifically valid because they are not observable, measurable, or consistent. They point to psychological phenomena like confirmation bias as explanations for why people perceive meaningful connections where none exist. However, the debate is far from settled. Whether you're a believer or a skeptic, the concept of synchronicity challenges us to question our understanding of the world. It invites us to explore the mysterious ways in which events in our lives might be interconnected, even if these connections defy conventional scientific understanding. Universal InterconnectednessIn a universe of endless possibilities, could it be that every choice, every thought, every coincidence is a dance of destiny? Synchronicity nudges us to ponder this profound question. Whether or not you believe in the concept, it challenges us to think about our place in the cosmos. Are we mere specks in an indifferent universe, or are we part of a grand cosmic symphony?
The concept of synchronicity opens up a realm of philosophical inquiry, inviting us to explore the interconnectedness of all things. It leaves us with a sense of wonder and curiosity, encouraging us to continue questioning, exploring, and seeking meaning in the mysterious dance of life. And there you have it—a deep dive into the enigmatic world of synchronicity. Whether you're a believer or a skeptic, one thing's for sure: the universe, and our place in it, is full of mysteries waiting to be explored. Humans innately search for meaning, often represented through personal timelines. The Fibonacci Lifechart provides an innovative lens to study synchronicity, merging mathematical modeling with stringent scientific standards. In a 2018-2019 research project, "The Predictability of Synchronicity," I compared synchronicity experiences of Jungian analysts with Fibonacci time patterns. With the hypothesis that synchronicity is a fractal resonance between the brain and environment, I expected a correlation. The findings, featured in the International Journal of Psychological Studies (Sacco, 2019), suggest that these coincidences might indeed be fractal resonance occurrences. Simply put, fractals are universal patterns reflecting energy and information exchanges. These patterns, underpinned by the Fibonacci series and the golden ratio, hint at a transfer of resonant frequencies beyond our usual realm. Echoed in everything around us, this resonance might explain life's profound coincidences. With life's essence potentially in these frequencies, and consciousness possibly anchored in the golden ratio's fractals (Pletzer et al., 2010), further research is essential to decode the true influence of these patterns on our lives. The Fibonacci LifechartThe Fibonacci sequence, a pattern evident in nature from seashells to galaxies, is deeply intriguing. Found in DNA, brain waves, and even the stock market, this sequence, alongside the golden ratio, holds mystery and potential. Might it also pave the way for studying synchronicity? Carl Jung, in a 1956 letter, pondered this very idea. Jung viewed the Fibonacci sequence as a link between mind and matter, essential for deciphering synchronicity (Jung, 1976). Influenced by quantum physicist Wolfgang Pauli, Jung's perspective on Fibonacci was unique, yet largely overlooked in synchronicity research. It's only now that its relevance in human development is being probed. During my psychotherapy practice, I stumbled upon a mathematical framework: The Fibonacci Lifechart, inspired by John Waskom and Norman Rose's exploration of Fibonacci's stages in human growth. Crafting this Lifechart, I delved into world religions, philosophies, and psychology, examining teachings from Taoism to Plato and insights from Jung to Erikson. In 2013, I showcased how the Fibonacci sequence could predict pivotal life events and phases (Sacco, 2013), like puberty, happiness peaks, and spirituality. My research juxtaposed two mathematical synchronicity models, suggesting synchronicity stems from a synergy between micro and macro dynamics. The Fibonacci sequence's nonlinear growth can symbolize both sequence and circularity. This circularity is subtly woven into Fibonacci, exemplified by the 5th number being five and the 12th being 144 (12x12). The Fibonacci Life Chart Method (FLCM) postulates that the brain and environment harmoniously resonate due to shared fractal geometries based on the golden ratio. This mutual resonance might be the seed for meaningful coincidences. World’s First Scientific Proof of Synchronicity?In January 2018, over a friendly chat, Bernard Beitman and I discussed starting a Journal on Coincidence. Bernard was all ears and really encouraging. But as we delved deeper, we realized that many existing journals didn't have much research on meaningful coincidences. Rather than starting from scratch, Bernard supported my curiosity to explore a theory I had: the connection between Fibonacci patterns and synchronicity. It was a delightful exchange of ideas, and I was grateful for his backing. In February 2018, I launched the Synchronicity Survey targeting the International Association for Analytical Psychology (IAAP) members. The goal was to explore the alignment between Jungian analysts' synchronicity experiences and Fibonacci time patterns. This was my investigation into the correlation of Fibonacci time patterns with synchronicity. Impressively, Fibonacci timelines mirrored theoretical synchronicity predictions within a ±34 days margin. Simple surveys, often overlooked, have shed light on understanding synchronicity. However, the results warrant cautious interpretation. Notably, the study highlighted significance at a 10% level, deviating from the conventional 5% standard. While some see merit in this (especially with limited sample sizes), others argue for discarding p values as sole significance markers (Wasserstein, Schirm, & Lazar, 2019). The small sample size—41 synchronicity instances among 18 participants—further calls for expanded research. The study's select demographic—Jungian analysts more attuned to meaningful coincidences—might limit its broader applicability. Personality traits, potentially correlated with demographic attributes, might influence synchronicity experiences. Identifying these traits could boost the predictive accuracy of the Fibonacci Lifechart. Yet, it's undeniable: Fibonacci algorithms and surveys are transforming synchronicity research. Emerging fields like quantum computing and biology are reshaping our universe's understanding, blending science with spirituality. Personally, the Fibonacci Lifechart has spurred my growth, and I'm delighted to share this tool. It's freely accessible at www.fibonaccilifechart.com. ReferencesJung, C. G. (1976). Letters of C.G. Jung (Vol. 2). London: Routledge and Kegan Paul.
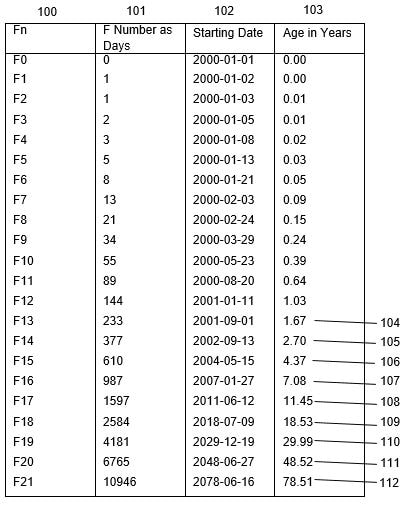
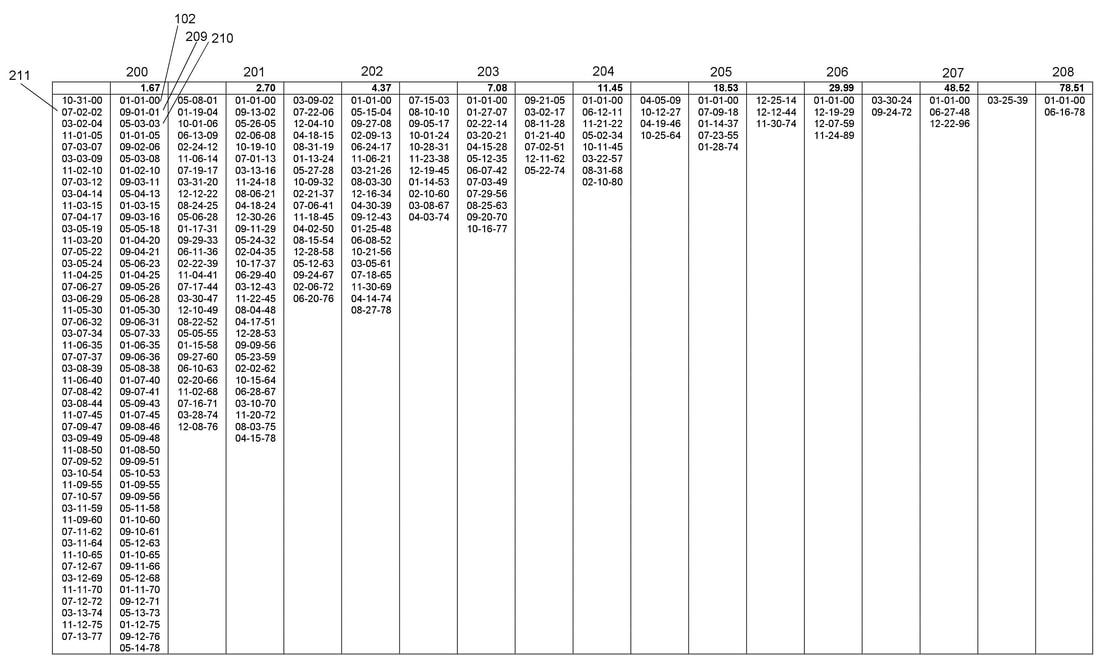
Livio, M. (2008). The golden ratio: The story of Phi, the world’s most astonishing number. New York, NY: Broadway Books. Pletzer, B., Kerschbaum, H. & Klimesch, W. (2010). When frequencies never synchronize: The golden mean and the resting EEG. Brain Research, 1335, 91-102. https://doi.org/10.1016/j.brainres.2010.03.074 Sacco, R.G. (2013). Re-envisaging the eight developmental stages of Erik Erikson: The Fibonacci Life-Chart Method (FLCM). Journal of Educational and Developmental Psychology, 3(1), 140–146. https://doi.org/10.5539/jedp.v3n1p140 Sacco, R. G. (2019). The predictability of synchronicity experience: Results from a survey of Jungian analysts. International Journal of Psychological Studies, 11(3), 46-62. https://doi.org/10.5539/ijps.v11n3p46 Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “p< 0.05”. The American Statistician, 73(sup1), 1-19. In a piece I authored in June 2018 (Sacco, 2018), I introduced a technique designed to forecast synchronistic events, be it within counseling sessions or for personal introspection. By employing this approach, individuals can attain a more profound comprehension of the synchronicities that have colored both their past and present. In this blog post, I'll further unpack the nuances of this technique, which I've called the "Harmonic Model." Background Carl Jung (1952) characterized synchronicity as the consequential overlap between external and internal occurrences. He refined his perspective on synchronicity in collaboration with the renowned quantum physicist, Wolfgang Pauli. Synchronicities stand apart as acausal events, meaning they don't align with traditional cause-and-effect paradigms. Jung coined the term "synchronicity" as a canopy concept, encapsulating various paranormal instances within its ambit. These events often defy regular causality, and are occasionally labeled as superstitious, magical, or supernatural. "Synchronization" references the spontaneous manifestation of order in intricate systems, marked by distinct geometric patterns and an almost periodic structure (Pikovsky, Rosenblum, & Kurths, 2001). Notably, contemporary research underscores the pivotal roles of Fibonacci numbers and the golden ratio in synchronization. The Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21, and so on) evolves recursively, where each number is the summation of its two predecessors. An intriguing mathematical relationship emerges between the Fibonacci sequence and the golden ratio (approximately 1.618034). As one progresses through the Fibonacci numbers, the ratio of successive numbers tends to converge on the golden ratio. Delving deeper into the enigma of synchronicity, the path forward lies in crafting theories that demystify the origins of such experiences. Since Jung's introduction of the synchronicity theory (Jung, 1952), scholars have grappled with conceptualizing a comprehensive model for this phenomenon. Drawing from Sacco's works (2016, 2018), it's posited that Fibonacci numbers hold the potential to forecast synchronistic events (Sacco, 2016). In the ensuing section, I will detail the methodology crafted to realize this intriguing proposition. Summary of Harmonic Model The Harmonic Model offers a robust framework for predicting the phenomena of synchronicity. By grasping the origin and nature of synchronistic events, researchers and clinicians can more effectively harness transformative processes. Central to this model is the role of Fibonacci numbers. These numbers, which permeate from the quantum realm to DNA structures, biological cell divisions, and even self-organizing systems, serve as powerful predictors of both physical and psychological shifts. Notably, they shed light on increases in synchronistic experiences. Employing a computer-assisted approach, the Harmonic Model forecasts synchronicity throughout human life. The methodology involves: 1. Inputting a birthdate; 2. Computing primary intervals by augmenting the birthdate with the initial 21 Fibonacci numbers, where each Fibonacci number equates to a 24-hour timeframe; 3. Deriving secondary intervals, which employ dates from the previous step to establish standing wave harmonics. These harmonics manifest when the primary intervals recur consistently up to age 78.51 or another predetermined endpoint; 4. Representing these intervals graphically. For counselors, the Harmonic Model becomes a tool of insight and guidance: 1. They plot the computed time intervals; 2. Analyze the ensuing graphical representation; and 3. Provide counsel tailored to the insights derived from the model. Harmonic Model-based counseling offers a holistic methodology, integrating diagnostic components with clear guiding principles for interventions. Illustrative figures provided alongside further elucidate these advantages and the model's broader implications. Figure 1: Primary interval calculations Figure 1 presents the primary interval calculations based on a birthdate of January 1, 2000 (depicted as 102). Here's a breakdown: 1. The Fibonacci sequence displays its first 21 numbers, labeled as (100). 2. In the stage marked by 101, these initial 21 Fibonacci numbers are translated to correspond with a 24-hour clock format. 3. Step 102 involves adding these Fibonacci numbers to the individual's birthdate. 4. The subsequent age accumulation, expressed in years, is illustrated in step 103. Figure 2: Secondary interval calculations. Figure 2 showcases the secondary interval computations of the Harmonic Model, which are built upon the primary interval calculations (represented as 103). Here's an elucidated breakdown: 1. The secondary date calculations, denoted as (200-208), stem from the final nine primary interval computations (104-112). 2. These secondary intervals are obtained by adding the primary intervals, beginning from the birthdate. 3. To illustrate, the computation for the secondary interval on 2003-05-03 [210] is derived from 2001-09-1 [209] by adding 1.67 years (sourced from 104). 4. These calculations exemplify the nodal points characteristic of standing wave harmonics. 5. The antinodes, marked as [211], are computed using the mean values of the neighboring nodes. The Fibonacci Lifechart presents the secondary interval computations in two formats: a cycle plot, as depicted in Figure 2, and a sequential listing. By juxtaposing both the cycle plot and the chronological list of dates against the seven life domains (namely residence, cohabitation, intimate relationships, family, occupation, health, and spiritual experience), one can assess instances of synchronicity experiences. Click here to get a copy of the Fibonacci Lifechart. References Coldea, R., Tennant, D. A., Wheeler, E. M., Wawrzynska, E., Prabhakaran, D., Telling, M.,... Kiefer, K. (2010). Quantum criticality in an Ising chain: Experimental evidence for emergent E8 symmetry. Science, 327(5962), 177-180. http://sci-hub.tw/10.1126/science.1180085
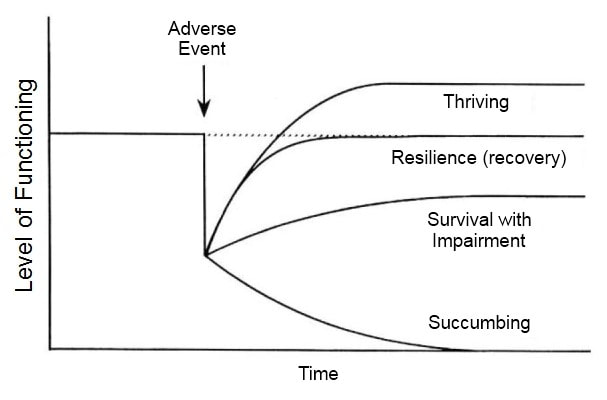
Jung, C. G. (1952). Synchronicity: An acausal connecting principle. CW 8. Pikovsky, A., Rosenblum, M., & Kurths, J. (2001). Synchronization: A universal concept in nonlinear sciences. Cambridge, UK: Cambridge University Press. Pletzer, B., Kerschbaum, H., & Klimesch, W. (2010). When frequencies never synchronize: The golden mean and the resting EEG. Brain Research, 1335, 91-102. http://sci-hub.tw/10.1016/j.brainres.2010.03.074 Sacco, R. G. (2016). The Fibonacci Life-Chart Method (FLCM) as a foundation for Carl Jung’s theory of synchronicity. Journal of Analytical Psychology, 61(2), 203-222. http://sci-hub.tw/10.1111/1468-5922.12204 Sacco, R. G. (2018). Fibonacci harmonics: A new mathematical model of synchronicity. Applied Mathematics, 9, 702-18. http://sci-hub.tw/10.4236/am.2018.96048 Sacco, R.G. (2019). Modeling celestial mechanics using the Fibonacci numbers. International Journal of Astronomy, 8, 8-12. http://sci-hub.tw/10.5923/j.astronomy.20190801.02 The mystical experience has been a topic of profound interest and exploration throughout history. William James, a trailblazer in the examination of such experiences, eloquently described the journey as an "organic ripening." While various scholars have presented nuanced stages of the mystical journey, they converge on key elements that mirror the stages of a psychological crisis. These stages invariably encompass: - Encountering unforeseen stressful life events, - A transient decline in one's usual functioning, - The potential for significant personal and spiritual evolution. In my work, "Mystical Experience: A Psychological Perspective," I delineated a five-phase crisis model, capturing the essence of this transformative journey: 1. Pre-crisis 2. Impact 3. Crisis 4. Resolution 5. Post-crisis In this piece, I shall delve deeper into these quintessential phases. It's pivotal to understand, though, that no singular model can wholly encapsulate the fluidity and diversity of mystical experiences. The journey may sometimes see phases rapidly transitioning, at times some phases might appear skipped, or occasionally one might find themselves anchored at a specific stage. Yet, the inherent strength of this crisis model is its capacity to formulate testable hypotheses, paving the way for rigorous empirical research. Phase 1: The Equilibrium Phase (Pre-Crisis) In this phase, individuals find themselves in a balanced state, where stressors are countered effectively by their coping mechanisms. Continuously tackling problems, individuals remain poised as long as they trust their abilities to manage challenges, ensuring stability. Phase 2: The Disruption Phase (Impact) This phase marks the onset of a psychological crisis, triggered by sudden interruptions to vital life goals, which elude standard problem-solving techniques. Such disruptions might arise from: - Strained personal relations - Job losses - Financial strains - Life-altering changes - Bereavements - Dire health diagnoses During the initial 1-3 days, individuals grapple with shock, confusion, and a profound sense of vulnerability amidst tumultuous emotions. It's vital to understand that the external events in themselves aren't the crisis; the individual's emotional and psychological reactions give the event its weight. Phase 3: The Turmoil Phase (Crisis) Following the initial shock, a turbulent period ensues, typically lasting 1-3 months. Marked by heightened anxiety, irritability, fatigue, despondency, and sleep disturbances, individuals confront the pressing challenge head-on. As conventional strategies falter, feelings of anxiety, desolation, and hopelessness surge. Gradually, individuals grapple with profound existential dilemmas, wrestling with a quest for elusive "truths" and gravitating towards non-linear guidance. Phase 4: The Intuitive Response Phase (Resolution) During this phase, all efforts pivot towards mitigating distress. However, decision-making leans heavily on instinctual reactions over analytical reasoning. Notably, not all resolutions prove beneficial. As William James pointed out, mystical experiences can traverse the spectrum from enlightening to darkly unsettling. A holistic understanding of mystical experiences should recognize the potential for both uplifting and detrimental consequences. Phase 5: The Rebuilding Phase (Post-Crisis) Stretching over a span of 2-12 months, this phase signifies a time of renewal, reconstruction, and recalibration. It witnesses profound, occasionally stark, transformations in the individual's being. An equilibrium, albeit altered, is achieved. It may either dip below, match, or exceed the pre-crisis level. The aftermath of a crisis can be visualized through four distinct trajectories: 1. Succumbing: Overwhelmed by the crisis, individuals might find their capacities diminished, ultimately feeling defeated. 2. Survival with Impairment: Here, individuals pull through, but with noticeable deficits or limitations. 3. Resilience: In this scenario, individuals bounce back, reclaiming their pre-crisis state. 4. Thriving: The most empowering outcome, individuals not only recover but ascend beyond their prior state, embodying traumatic growth. Figure 4. Four possible outcomes of adversity Mystical experiences frequently usher in profound and enduring positive transformations. These transformative effects can be categorized into four domains: self-awareness, interpersonal relationships, life perspective, and understanding of the mystical experience itself.
1. Self-awareness: While a mystical experience doesn't necessarily alter the foundational personality traits, it powerfully reshapes one's aspirations, emotions, attitudes, behaviors, and overall life purpose. This is akin to a personal metamorphosis, redefining one's essence and direction. 2. Interpersonal Relationships: Post such an experience, individuals tend to exhibit greater openness, authenticity, and tolerance, enhancing their connections with others. Their interactions become more genuine and empathetic. 3. Life Perspective: One of the most profound shifts is in the perception of life itself. Mystical experiences frequently instill a renewed sense of hope, making purpose and meaning more palpable in day-to-day existence. Life is seen through a lens of deeper significance and interconnectedness. 4. Understanding Mystical Experiences: Finally, individuals develop a more profound comprehension of the integral role mystical experiences play in life's grand tapestry. They come to value these moments not as anomalies but as crucial chapters in their life story. So, should you ever find yourself in the throes of a stressful event, questioning the essence of existence, remember: it might just be the prelude to an illuminating transformation. A journey that might elevate your understanding of life to dimensions beyond your wildest imaginations. One may say truly, I think, that personal religious experience has its root and center in mystical states of consciousness. —William James (1902, p. 379) Have you ever had a mystical experience? What separates a mystical experience from an ordinary one? The Core of Mystical Experience The cornerstone of mystical experiences, as researchers concur, is the profound sensation of unity. At the heart of debates surrounding mystical experiences lies the interpretation of this unity. How do we understand or express this overwhelming oneness? A seminal reference in Western studies of mystical experiences is William James's "Varieties of Religious Experience." James posits that these moments, though infrequent, represent episodes where individual consciousness coalesces in an overwhelming unity with the cosmos. James delineated four hallmarks of mystical experiences: 1. Ineffability - The indescribable nature of the experience. 2. Noetic Quality - A deep, insightful knowledge or realization. 3. Transiency - The fleeting nature of the experience. 4. Passivity - A feeling of being overtaken or grasped by a force beyond one's control. James's pioneering work underscores the distinctiveness of mystical experiences, setting them apart from our routine experiences. His insights laid the groundwork, setting an exemplary standard for contemporary explorations into the realm of mystical experiences. Introvertive and Extrovertive Unity One of the enduring queries that has followed William James's exploration is: What precisely constitutes the mystical experience of unity?
Stace (1960) proposed that this enigmatic experience of unity manifests in two distinct ways: the "introvertive" and the "extrovertive." The introvertive unity is an introspective journey, where the individual delves deep into the mind, reaching a state of "pure consciousness." It's often encountered during meditation with closed eyes and is characterized by a profound sense of emptiness or nothingness. Conversely, the extrovertive unity is an outward-facing experience. As described by Stace (1960, p. 110), the individual "looks outward through the senses," recognizing the interwoven tapestry of existence, finding unity in the diverse fabric of the natural world. Here, everything, from stones and trees to the vast expanse of the sky, is felt to pulsate with life. Delving into related phenomena, the term "synchronicity," introduced by renowned psychologist Carl Jung, describes moments where an external event resonates deeply with one's inner state. These synchronistic episodes lack a causal link between the tangible event and the internal experience. This concept aptly encapsulates the extrovertive facet of the mystical experience. |



 RSS Feed
RSS Feed