|
In the realm of understanding, where concepts intertwine like threads in a grand web, the idea of recursion stands as a pillar, echoing the patterns found in nature, mathematics, and the very fabric of reality. This exploration delves into the profound interconnectedness of recursion, the eternal now, unraveling time, fractal understanding, and the cause and effect, woven together in a feedback loop that mirrors the infinite complexity of the Fibonacci sequence. Figure 1. Recursion and the Eternal Now: This figure presents a journey through recursion, the eternal now, unraveling time, and fractal understanding, all linked by cause and effect within an ongoing feedback loop. Inspired by Fibonacci recursion, it shows how each concept fluidly transitions into the next, reflecting universal patterns. This visual exploration invites us on a discovery where time and consciousness blend, unveiling the interconnected weave of reality. The Foundation: Recursion and Fibonacci Recursion, at its core, is a method where the solution to a problem depends on solutions to smaller instances of the same problem. It's a principle beautifully exemplified by the Fibonacci sequence, where each number is the sum of the two preceding ones. This sequence is not just a mathematical curiosity but a pattern that recurs throughout nature, from the spirals of shells to the branching of trees. In our conceptual framework, recursion represents the starting point, the seed from which our understanding of the eternal now begins. It's the process of looking inward, of finding within each moment the seeds of past and future, each now a reflection of the infinite recursion that defines our existence. The Eternal Now: Pure AwarenessAt the heart of our exploration lies the eternal now, a state of pure awareness unbound by the linear constraints of time. It's a concept that transcends the ticking of clocks and the pages of calendars, representing a moment of clarity and presence that is both fleeting and everlasting. This eternal now is not a static point but a gateway to deeper understanding, a lens through which we view the dance of interconnection that binds all things. It's in this eternal moment that we find the essence of recursion, the echo of the Fibonacci sequence in the rhythm of our thoughts and the patterns of our consciousness. Unraveling Time: The Dance of Interconnection From the eternal now, we move to the unraveling of time, a process that reveals the interconnected nature of our experiences and perceptions. Time, in this context, is not a line but a web, a complex weave of causes and effects that defy simple linear explanation. This unraveling is a journey through the fractal complexity of reality, where each moment contains within it the seeds of countless others. It's a recognition that every event, every thought, and every action is part of a greater whole, a symphony of interconnection that resonates with the patterns of recursion and the Fibonacci sequence. Fractal Understanding: Beyond Cause and Effect As we delve deeper into the web of time, we arrive at fractal understanding, a perspective that transcends the traditional linear chain of cause and effect. In this realm, the simplicity of one-to-one relationships gives way to a more fluid, dynamic understanding of how things relate. Fractal understanding is about recognizing the self-similar patterns that recur at different scales, from the microcosm to the macrocosm. It's about seeing the Fibonacci sequence not just in a series of numbers but in the very structure of our thoughts and the universe itself. The Feedback Loop: A Return to Recursion Completing our conceptual journey is the feedback loop, a path that leads from the complexities of fractal understanding back to the simplicity of recursion. This loop is a reminder that in every end is a beginning, in every complexity, a simplicity waiting to be discovered. The feedback loop is the breath of the cosmos, the rhythm of existence that dances to the tune of the Fibonacci sequence. It's a cycle of renewal and understanding that brings us back to the eternal now, enriched by our journey through the unraveling of time and the depths of fractal understanding. Conclusion: The Web of UnderstandingIn this exploration of recursion, the eternal now, and the fractal nature of reality, we find a reflection of the infinite complexity and beauty of the universe. Like the Fibonacci sequence, our understanding unfolds in ever-expanding spirals, each turn revealing new vistas of awareness and connection.
The journey through these concepts is not just an intellectual exercise but a meditation on the nature of existence itself. It's a reminder that in the patterns of the universe, from the smallest shell to the vastness of the cosmos, lies a message of interconnection and eternal renewal, a symphony of patterns waiting to be discovered and understood.
0 Comments
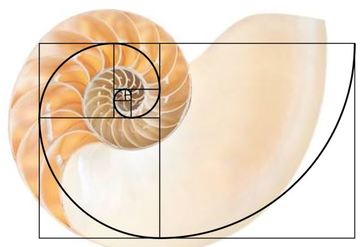
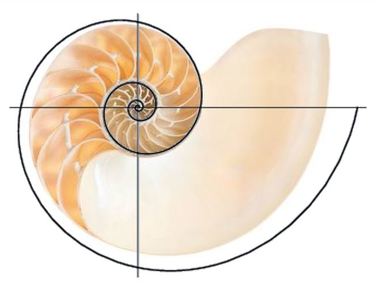
The Fibonacci sequence is a marvel that has captivated mathematicians throughout history. But its allure extends beyond math, influencing fields like art, biology, architecture, music, botany, and finance. Is this truly the world's most mesmerizing number sequence, or are we stretching our imagination to find patterns where none lie? Join us as we delve deep into this mathematical wonder that has fascinated minds across disciplines and eras. 1. Does Architectural design reflect the golden ratio? The golden ratio is often touted as appearing in many architectural marvels, both ancient and contemporary. Examples span from the Great Pyramid of Giza and the Parthenon to modern landmarks like the Eiffel Tower, Toronto’s CN Tower, and the United Nations Secretariat building. It's debated whether all these structures consciously employ the golden ratio in their designs. The Parthenon, with its intricate layout, leaves us guessing about its architects' intentions regarding the golden ratio. However, there seems to be a deliberate use of the golden ratio in the design of Toronto’s CN Tower. The proportion between its total height (553.33 meters) and the height to its observation deck (342 meters) is strikingly close to 1.618, the golden ratio. The CN Tower is a communications tower built in 1976. It was the world’s tallest free-standing structure at the time. 2. Is the spiral of the Nautilus shell based on the golden ratio? Indeed, there's more nuance than popular narratives suggest. The classic "golden spiral" is crafted using consecutive golden rectangles, resulting in a spiral that expands by the golden ratio for every quarter turn. However, the Nautilus shell's spiral isn't an exact match to this golden spiral. The spiral constructed from a Golden Rectangle is NOT a Nautilus Spiral. Here's the crux of the matter: The golden ratio can shape spirals in multiple ways. For instance, a spiral that widens according to the golden ratio after every 180-degree twist more closely mirrors the spirals found in numerous Nautilus shells. A spiral expanding by the golden ratio at every 180-degree turn is a closer match to some Nautilus shells for the first few rotations I trust you grasp the distinction.
Here's another intriguing insight: The nautilus shell expands according to the number 108 (refer to "The Number 108"). This number resonates with the pentagram, which fundamentally operates on the principles of the golden ratio. Thus, it's evident that the Nautilus spiral can indeed reflect proportions approaching Phi. 3. Did renaissance artists use the golden ratio in their paintings? Absolutely. Leonardo Da Vinci's "Last Supper" prominently features golden ratios. Inspired by him, Salvador Dalí, in 1955, crafted "The Sacrament of the Last Supper" adhering to golden ratio dimensions. Similarly, in Michelangelo’s "Creation of Adam," the iconic touch between God’s and Adam’s fingers occurs exactly at the golden ratio point of the width within their frame. These instances highlight just a fraction of the Renaissance artists' fascination with the golden ratio in their masterpieces. 4. Are the spirals seen in nature based on the golden ratio? Spirals in nature are often linked to the golden ratio, and while it's not universally true, there are noteworthy instances. Sunflower seeds, for instance, form interconnecting spirals based on Fibonacci numbers. This Fibonacci-driven pattern maximizes the number of seeds on a seed head. Beyond sunflowers, the golden ratio influences the growth of leaves, branches, and petals, optimizing sunlight absorption as new leaves emerge. Nature frequently showcases logarithmic spirals: from spiral galaxies and ram horns to hurricanes and whirlpools. The golden spiral is a subset of these logarithmic spirals, and while it may be present in the examples listed, not all natural logarithmic spirals are golden spirals. 5. Is there a new algorithm based on the golden ratio that can predict spiritual experience? It seems that there might be a connection between mathematics and spiritual experience. Sacco's 2017 study tentatively suggested that the dynamic effects observed at age 18 could potentially predict an elevation in spiritual experiences. This observation aligns with the predictions of the FLCM. This offers a tentative link between the relationship of the golden ratio and spiritual experience. However, the dynamical effects of age 11 and 30 did not support the hypothesis of increased spiritual experience as predicted. This result required an alternative explanation. It should be evident that children at age 11 may not be able to communicate the complexities of some spiritual experiences. And it’s entirely reasonable that spiritual experiences could be linked with the instability that is less likely at age 30 when personality becomes stabilized. In the real world, there are many compelling examples of the golden ratio in natural phenomena. But not all phenomena in nature are based on the golden ratio. You can find plenty of examples where the golden ratio is not found in nature as might be expected. But you can’t deny the power of data and evidence to prove the inherent power of the golden ratio in reality. The critical question you need to ask yourself is: Why does the golden ratio show up so commonly in nature? The Golden Ratio: A Principle of Energy Flow The golden ratio, seen in structures as vast as galaxies or as intricate as DNA, has long been the symbol of ideal harmony. Duke University's Adrian Bejan ties this unique ratio to a universal law of nature's design. Through his work on the constructal law, Bejan reveals how nature shapes itself to ease flow. The essence of the golden ratio, he suggests, lies in achieving maximal efficiency with minimal energy (Bejan, 2009). This ratio allows structures to scale infinitely without changing their core shape, resulting in its recurrence throughout nature. By choosing the path of least resistance, the golden ratio epitomizes energy-efficient flow. This is evident in falcons, which harness the golden spiral for an energy-saving approach to their prey (Tucker, 2000), and in plants, where Fibonacci spirals display energy optimization in phyllotaxis (Li et al., 2007). The Purpose of Life: Flow The Constructal Law intertwines modern science with ancient spiritual writings, hinting at a unified purpose for all existence: to facilitate energy flow. Energy naturally seeks equilibrium, flowing from concentrations, like the sun, to the expansive universe. Our individual purpose is deciphering our unique energy flow. Despite being made of the same elements, each person's energy interplays differently. Our brains might share a similar number of nerves, but the connections, molded by experiences, are distinct, crafting our personalities. When our energies align, we enter a "flow" state, a concept explored by Csikszentmihalyi (1990) and Maslow (1964). In this state: Causes of Flow: - Clear goals - Immediate performance feedback - Confidence in handling challenges Characteristics of Flow: - Absolute focus - Control and openness - Enhanced learning and positivity Consequences of Flow: - Transcendence of self-awareness - Altered time perception - Intrinsic reward from the activity Discovering your energy's optimal flow—whether through passions or talents—uncovers your unique life purpose. Like fingerprints, our energy patterns are singular. Aligning with this flow often leads to peak performance, happiness, and fulfillment, underscoring our individual roles in the universe. References
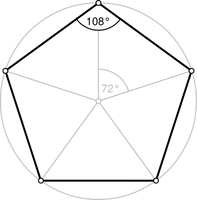
Bejan, A. (2009). The golden ratio predicted: Vision, cognition and locomotion as a single design in nature. International Journal of Design & Nature and Ecodynamics, 4(2), 97-104. Csikszentmihalyi, M. (1990). Flow: The Psychology of Optimal Experience. Harper and Row, New York, NY. Li, C., Ji, A., & Cao, Z. (2007). Stressed Fibonacci spiral patterns of definite chirality. Applied Physics Letters, 90(16), 164102. Maslow, A. H. (1964). Religions, values, and peak-experiences. Columbus, OH: Ohio State University Press. (Original work published 1940) Tucker, V. A. (2000). The deep fovea, sideways vision and spiral flight paths in raptors. Journal of Experimental Biology, 203(24), 3745-3754. The Sacred Significance of "108" The number "108" holds profound significance across various spiritual traditions. In Hinduism and Buddhism, it represents a path of balance with 108 virtues to nurture and 108 defilements to shun. This sense of equilibrium extends to their malas (or rosaries), which feature 108 beads. In Islamic traditions, "108" is sometimes invoked in place of God's name. Even in tai chi, a practice rooted in fluid motion and balance, there are 108 movements. The recurring presence of this number across diverse spiritual practices suggests its importance goes beyond mere coincidence. 108 and Growth The number 108 has intriguing ties to the cosmos: the average distance from the Sun and Moon to Earth is 108 times their respective diameters. Beyond this celestial connection, the natural world showcases 108 in the growth of a nautilus shell. As the nautilus matures, each new chamber of its shell expands to be 1.08 times larger than the previous one, crafting a mesmerizing logarithmic spiral on the shell's exterior. In the BBC Two documentary "The Code," Professor Marcus du Sautoy from the University of Oxford unveils the elegant spiral shell of the nautilus, which grows at a constant rate of 1.08. He delves into how spirals and the wonders of math manifest across nature. 108 and The Number 5 The number 108 is related to the number 5. The clue is related to the angle of the Pentagon, being 108˚. 108 and The Fibonacci Sequence The number 108 has a profound significance when looked through the lens of decimal parity, an ancient numerical system used by cultures like Egypt and India to discern the essence of numbers. Decimal parity simplifies numbers to single digits. Take 361: 3 + 6 + 1 = 10, and further, 1 + 0 = 1. Thus, 361's decimal parity is 1. Consider the Fibonacci Sequence's first 24 numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657. Applying decimal parity to this sequence yields a recurring pattern of 24 digits: 0, 1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1. The sum? A familiar 108. Intriguingly, this pattern mirrors the 1.08 growth constant the nautilus adopts for its spiral shell. The connection between nature's designs and ancient numerical systems is truly fascinating. |





 RSS Feed
RSS Feed