Method of Using Fibonacci Numbers to Predict Synchronicity

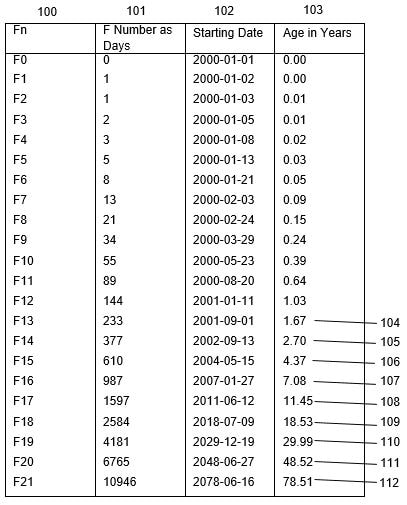
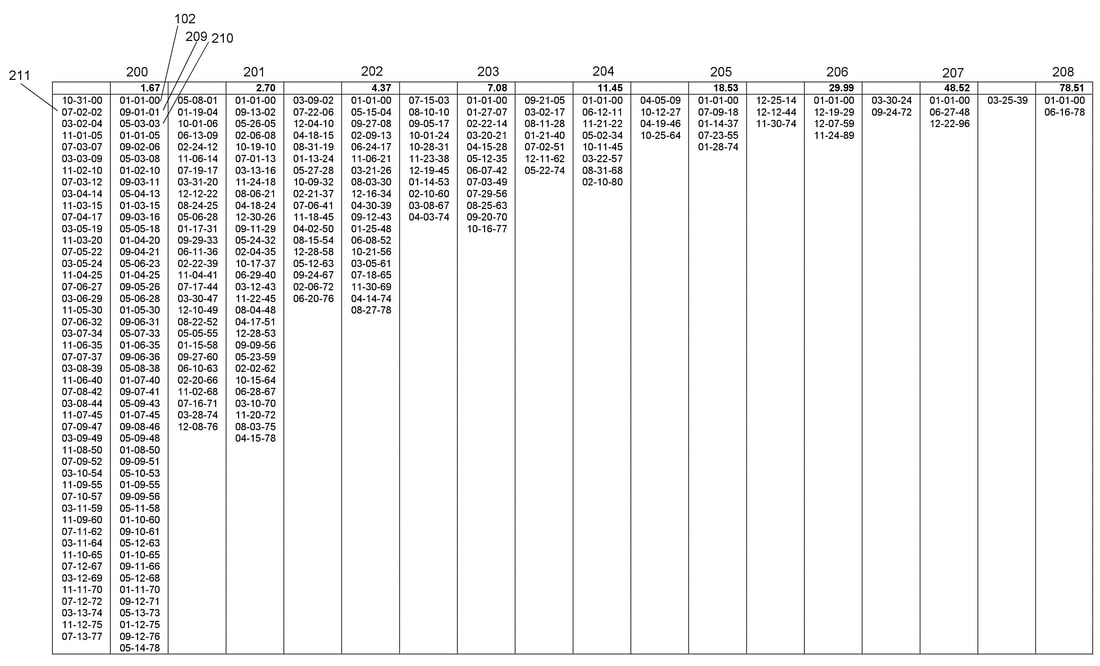
In a piece I authored in June 2018 (Sacco, 2018), I introduced a technique designed to forecast synchronistic events, be it within counseling sessions or for personal introspection. By employing this approach, individuals can attain a more profound comprehension of the synchronicities that have colored both their past and present.

In this blog post, I'll further unpack the nuances of this technique, which I've called the "Harmonic Model."

Background

Carl Jung (1952) characterized synchronicity as the consequential overlap between external and internal occurrences. He refined his perspective on synchronicity in collaboration with the renowned quantum physicist, Wolfgang Pauli.

Synchronicities stand apart as acausal events, meaning they don't align with traditional cause-and-effect paradigms. Jung coined the term "synchronicity" as a canopy concept, encapsulating various paranormal instances within its ambit. These events often defy regular causality, and are occasionally labeled as superstitious, magical, or supernatural.

"Synchronization" references the spontaneous manifestation of order in intricate systems, marked by distinct geometric patterns and an almost periodic structure (Pikovsky, Rosenblum, & Kurths, 2001). Notably, contemporary research underscores the pivotal roles of Fibonacci numbers and the golden ratio in synchronization.

The Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21, and so on) evolves recursively, where each number is the summation of its two predecessors. An intriguing mathematical relationship emerges between the Fibonacci sequence and the golden ratio (approximately 1.618034). As one progresses through the Fibonacci numbers, the ratio of successive numbers tends to converge on the golden ratio.

Delving deeper into the enigma of synchronicity, the path forward lies in crafting theories that demystify the origins of such experiences. Since Jung's introduction of the synchronicity theory (Jung, 1952), scholars have grappled with conceptualizing a comprehensive model for this phenomenon.

Drawing from Sacco's works (2016, 2018), it's posited that Fibonacci numbers hold the potential to forecast synchronistic events (Sacco, 2016). In the ensuing section, I will detail the methodology crafted to realize this intriguing proposition.

Summary of Harmonic Model

The Harmonic Model offers a robust framework for predicting the phenomena of synchronicity. By grasping the origin and nature of synchronistic events, researchers and clinicians can more effectively harness transformative processes.

Central to this model is the role of Fibonacci numbers. These numbers, which permeate from the quantum realm to DNA structures, biological cell divisions, and even self-organizing systems, serve as powerful predictors of both physical and psychological shifts. Notably, they shed light on increases in synchronistic experiences.

Employing a computer-assisted approach, the Harmonic Model forecasts synchronicity throughout human life. The methodology involves:

1. Inputting a birthdate;
2. Computing primary intervals by augmenting the birthdate with the initial 21 Fibonacci numbers, where each Fibonacci number equates to a 24-hour timeframe;
3. Deriving secondary intervals, which employ dates from the previous step to establish standing wave harmonics. These harmonics manifest when the primary intervals recur consistently up to age 78.51 or another predetermined endpoint;
4. Representing these intervals graphically.

For counselors, the Harmonic Model becomes a tool of insight and guidance:
​
1. They plot the computed time intervals;
2. Analyze the ensuing graphical representation; and 
3. Provide counsel tailored to the insights derived from the model.

Harmonic Model-based counseling offers a holistic methodology, integrating diagnostic components with clear guiding principles for interventions.

Illustrative figures provided alongside further elucidate these advantages and the model's broader implications.

Figure 1: Primary interval calculations

Figure 1 presents the primary interval calculations based on a birthdate of January 1, 2000 (depicted as 102). Here's a breakdown:

1. The Fibonacci sequence displays its first 21 numbers, labeled as (100).
2. In the stage marked by 101, these initial 21 Fibonacci numbers are translated to correspond with a 24-hour clock format.
3. Step 102 involves adding these Fibonacci numbers to the individual's birthdate.
4. The subsequent age accumulation, expressed in years, is illustrated in step 103.

Figure 2: Secondary interval calculations. ​​

Figure 2 showcases the secondary interval computations of the Harmonic Model, which are built upon the primary interval calculations (represented as 103). Here's an elucidated breakdown:

1. The secondary date calculations, denoted as (200-208), stem from the final nine primary interval computations (104-112).
2. These secondary intervals are obtained by adding the primary intervals, beginning from the birthdate.
3. To illustrate, the computation for the secondary interval on 2003-05-03 [210] is derived from 2001-09-1 [209] by adding 1.67 years (sourced from 104). 
4. These calculations exemplify the nodal points characteristic of standing wave harmonics.
5. The antinodes, marked as [211], are computed using the mean values of the neighboring nodes.

The Fibonacci Lifechart presents the secondary interval computations in two formats: a cycle plot, as depicted in Figure 2, and a sequential listing. By juxtaposing both the cycle plot and the chronological list of dates against the seven life domains (namely residence, cohabitation, intimate relationships, family, occupation, health, and spiritual experience), one can assess instances of synchronicity experiences.​
​Click here to get a copy of the Fibonacci Lifechart. 

References

Coldea, R., Tennant, D. A., Wheeler, E. M., Wawrzynska, E., Prabhakaran, D., Telling, M.,... Kiefer, K. (2010). Quantum criticality in an Ising chain: Experimental evidence for emergent E8 symmetry. Science, 327(5962), 177-180. http://sci-hub.tw/10.1126/science.1180085

Jung, C. G. (1952). Synchronicity: An acausal connecting principle. CW 8.

Pikovsky, A., Rosenblum, M., & Kurths, J. (2001). Synchronization: A universal concept in nonlinear sciences. Cambridge, UK: Cambridge University Press.

Pletzer, B., Kerschbaum, H., & Klimesch, W. (2010). When frequencies never synchronize: The golden mean and the resting EEG. Brain Research, 1335, 91-102. http://sci-hub.tw/10.1016/j.brainres.2010.03.074

Sacco, R. G. (2016). The Fibonacci Life-Chart Method (FLCM) as a foundation for Carl Jung’s theory of synchronicity. Journal of Analytical Psychology, 61(2), 203-222. http://sci-hub.tw/10.1111/1468-5922.12204

Sacco, R. G. (2018). Fibonacci harmonics: A new mathematical model of synchronicity. Applied Mathematics, 9, 702-18. http://sci-hub.tw/10.4236/am.2018.96048

Sacco, R.G. (2019). Modeling celestial mechanics using the Fibonacci numbers. International Journal of Astronomy, 8, 8-12. http://sci-hub.tw/10.5923/j.astronomy.20190801.02